前言
理论很烦人,一个术语就会扯出另一个术语、机器学习没有了术语,它啥也不是!
学习成本最大的就是在理解大量的生涩难懂的术语。然而大多情况下,并没有什么卵用。
理解这些术语和公式,无外乎能更深入理解算法的原理,参数的优化调整、甚至创建算法。
1、损失函数
损失函数(Loss Function )是定义在单个样本上的,算的是一个样本的误差。
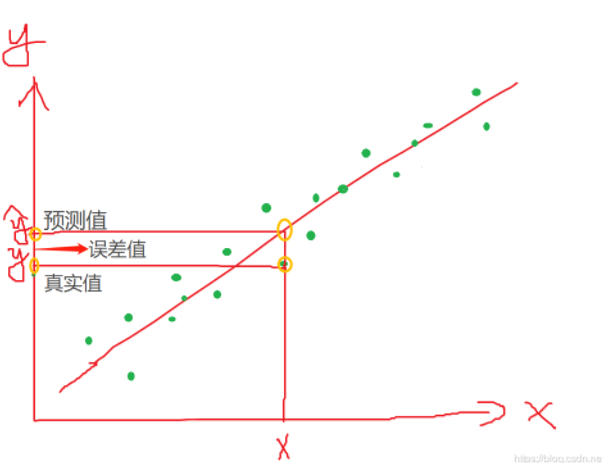


为每个样本的真实值y

为公式 g(x) = w1x1 + w2x2 + w3x3 + w4x4 +w0x0 的单个表现形式。
![]()
每个样本的误差值的表现形式
2、代价函数(Cost Function )
定义在整个训练集上的,是所有样本误差的平均,也就是损失函数的平均。
3、目标函数(Object Function)
定义为:最终需要优化的函数。等于经验风险+结构风险(也就是Cost Function + 正则化项)
损失函数我们通常用J来表示,例如,J(w) 则表示以 w 为自变量的函数。
在线性回归中,我们使用平方损失函数 (最小二乘法)(最小平方法),定义如下

2、岭回归
一种改良的最小二乘法,通过放弃最小二乘法的无偏性,以损失部分信息、
降低精度为代价获得回归系数更为符合实际、
更可靠的回归方法,它对病态数据的拟合要强于最小二乘法。
精度 =真正例/(真正例+假正例):也就是在所有判为恐怖分子中,真正的恐怖分子的比例。
召回率=真正例/(真正例+假反例): 也就是正确判为恐怖分子占实际所有恐怖分子的比例。
无偏性: 实际值和预测值相等时,叫做无偏性。
回归系数: 例如回归方程式Y=bX+a中,斜率b称为回归系数,表示X每变动一单位,平均而言,Y将变动b单位。
回归系数越大表示x 对y 影响越大,正回归系数表示y 随x 增大而增大,负回归系数表示y 随x增大而减小
模型误差 = 偏差(Bias)+ 方差(Variance)+ 数据本身的误差
偏差:导致偏差的原因有多种,其中一个就是针对非线性问题使用线性方法求解,当模型欠拟合时,就会出现较大的偏差
方差:产生高方差的原因通常是由于模型过于复杂,即模型过拟合时,会出现较大的方差
通常情况下,我们降低了偏差就会相应地使得方差提高,降低了方差就会相应地提高了偏差。
所以在机器学习的模型中,我们总是希望找到一组最优的参数,
这些参数能权衡模型的偏差和方差,使得模型性能达到最优
1、一般线性回归遇到的问题
在处理复杂的数据的回归问题时,普通的线性回归会遇到一些问题,主要表现在:
预测精度:这里要处理好这样一对为题,即样本的数量 n 和特征的数量 p
时,最小二乘回归会有较小的方差
时,容易产生过拟合
时,最小二乘回归得不到有意义的结果
模型的解释能力:如果模型中的特征之间有相互关系,这样会增加模型的复杂程度,并且对整个模型的解释能力并没有提高,这时,我们就要进行特征选择。 以上的这些问题,
主要就是表现在模型的方差和偏差问题上,这样的关系可以通过下图说明:
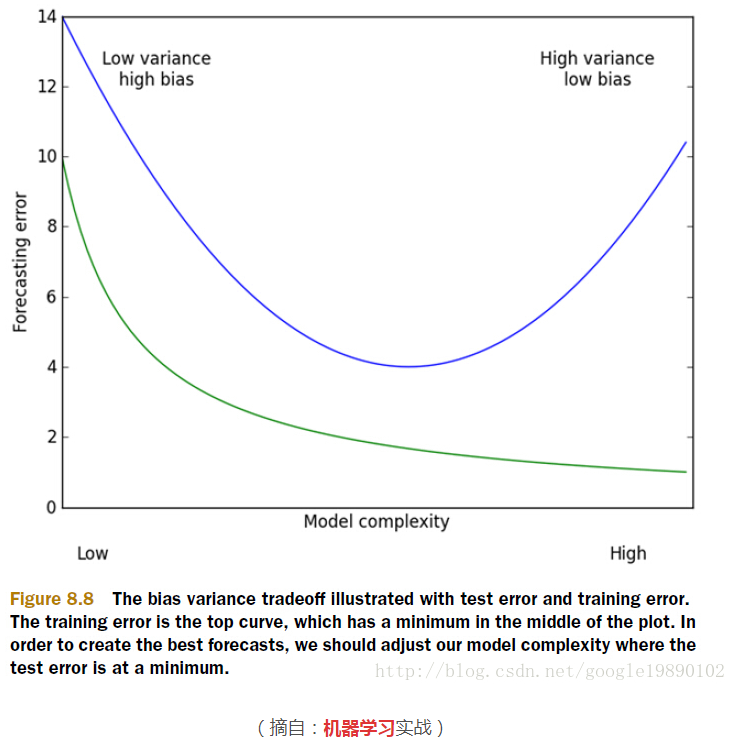
方差指的是模型之间的差异,而偏差指的是模型预测值和数据之间的差异。我们需要找到方差和偏差的折中
2、岭回归的概念
在进行特征选择时,一般有三种方式:
- 子集选择
- 收缩方式(Shrinkage method),又称为正则化(Regularization)。主要包括岭回归和lasso回归。
- 维数缩减
岭回归(Ridge Regression)是在平方误差的基础上增加正则项,
通过求导最终为:
3、岭回归 和 sklearn验证
针对高方差,即过拟合的模型,解决办法之一就是对模型进行正则化:限制参数大小
(由于本篇博客所提到的岭回归和Lasso都是正则化的特征选择方法,所以对于其他解决过拟合的方法不多赘述)
当线性回归过拟合时,权重系数wj就会非常的大,岭回归就是要解决这样的问题。
岭回归(Ridge Regression)可以理解为在线性回归的损失函数的基础上,加,入一个L2正则项,来限制W不要过大。
其中λ>0,通过确定λ的值可以使得模型在偏差和方差之间达到平衡,随着λ的增大,模型的方差减小,偏差增大。

我们可以像线性回归一样,利用最小二乘法求解岭回归模型的参数,对W求导,令倒数等于0,
可求得W的解析解,其中I为m x m的单位矩阵,
所以也可以说岭回归就是在矩阵X^TX上加一个λI使得矩阵非奇异,进而能对XTX+λI求逆:
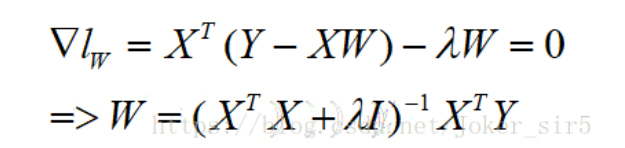
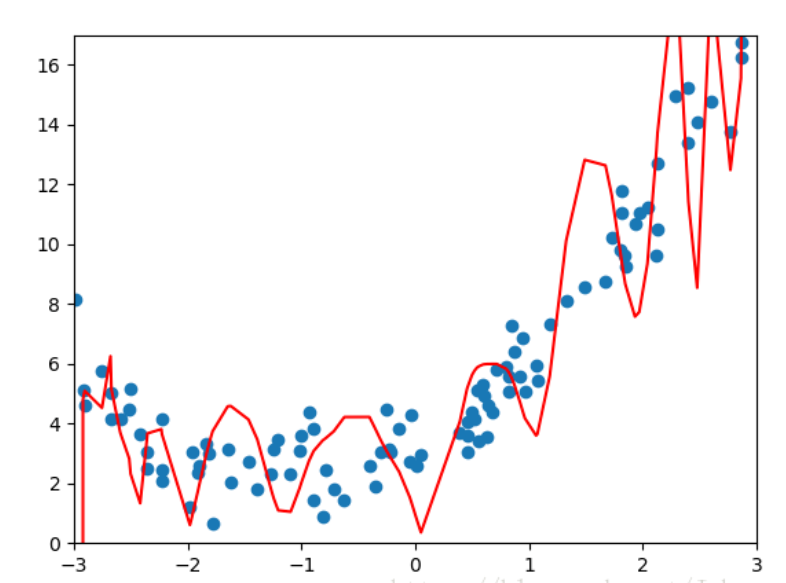
为了可视化,我们还引用上篇博客的测试用例,使用Pipeline封装多项式特征,归一化,线性回归方法,
为了说明问题并将PolynomialFeatures的参数degree调整到40,此时模型很明显得出现了过拟合,产生了高方差:
poly_reg = Pipeline([
("poly", PolynomialFeatures(degree=40)),
("std_scaler", StandardScaler()),
("lin_reg", LinearRegression())
])
使用sklearn封装的岭回归方法进行测试
poly_reg = Pipeline([
("poly", PolynomialFeatures(degree=40)),
("std_scaler", StandardScaler()),
("ridge_reg", Ridge(alpha=0.01))
])
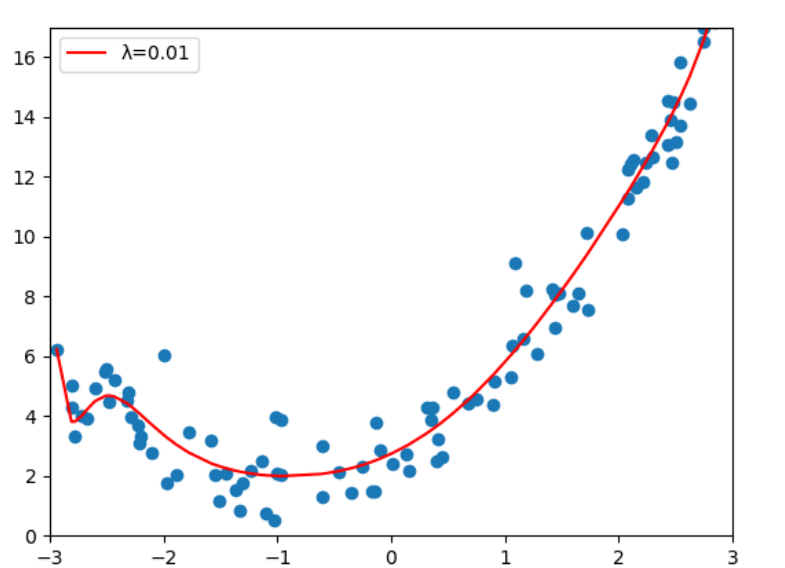
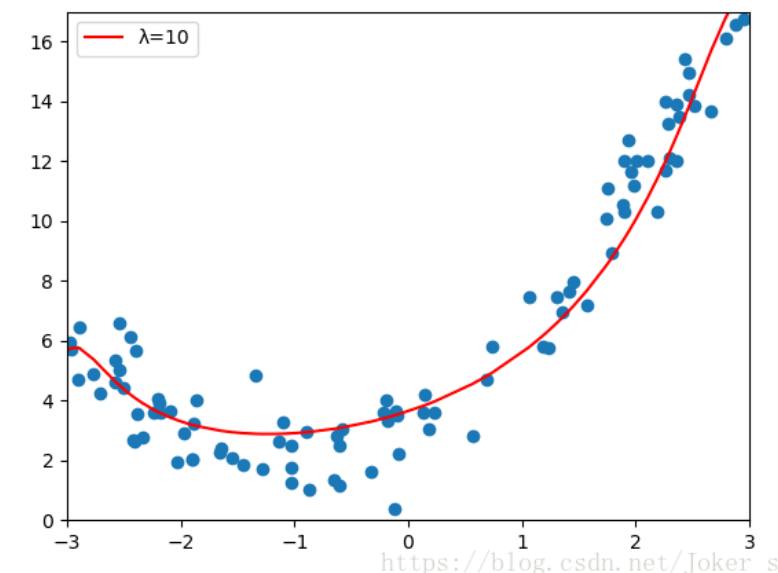
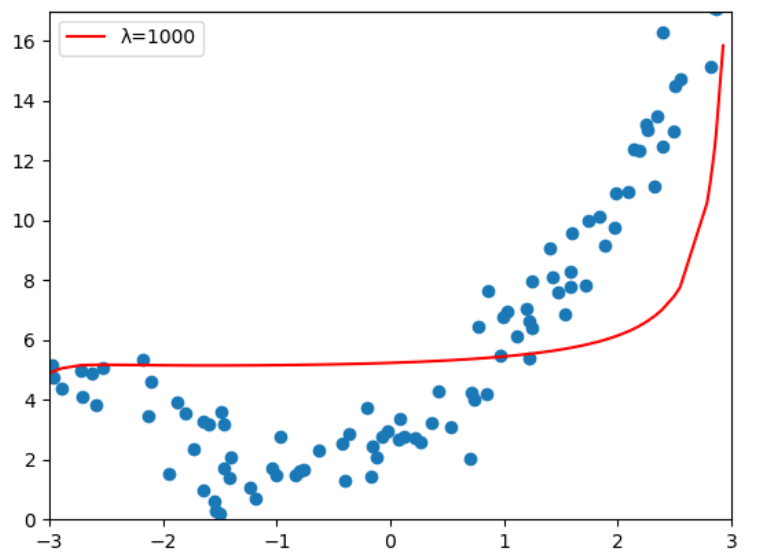
对比图中红线可以看到,λ=0.01时,虽然多项式特征的degree=40,相较于直接使用线性回归,
岭回归已经很好的解决高方差的问题,但λ不能过大,当λ=1000时明显的出现了欠拟合,
相应的模型的偏差也增大了,我们的目的就是要权衡偏差和方差,使模型达到最优。
 同乐学堂
同乐学堂
 微信扫一扫,打赏作者吧~
微信扫一扫,打赏作者吧~



