(1)什么是轮廓?
轮廓可以简单地解释为连接所有具有相同的颜色或强度的连续点(沿着边界)的曲线。
轮廓是形状分析和物体检测和识别的很有用的工具。
-
为了更好的准确性,使用二进制图像,因此,在找到轮廓之前,应用阈值或canny边缘检测。
-
从OpenCV 3.2开始,findContours()不再修改源图像,而是将修改后的图像作为三个返回参数中的第一个返回。
-
在OpenCV中,找到轮廓就像从黑色背景中找到白色物体。所以请记住,要找到的对象应该是白色,背景应该是黑色。
让我们看看如何找到二进制图像的轮廓:
import numpy as np import cv2 as cv im = cv.imread('test.jpg') imgray = cv.cvtColor(im, cv.COLOR_BGR2GRAY) ret, thresh = cv.threshold(imgray, 127, 255, 0) im2, contours, hierarchy = cv.findContours(thresh, cv.RETR_TREE, cv.CHAIN_APPROX_SIMPLE)
轮廓和层次结构。轮廓是图像中所有轮廓的Python列表。每个单独的轮廓是对象的边界点的(x,y)坐标的Numpy阵列。
注意:我们稍后将详细讨论第二和第三个参数以及层次结构。在此之前,代码示例中给出的值对所有图像都可以正常工作。
(2)如何绘制轮廓?
要绘制轮廓,可以使用cv.drawContours函数。如果图像有边界点,它也可以用于绘制任何形状。
它的第一个参数是源图像,第二个参数是应该作为Python列表传递的轮廓,第三个参数是轮廓索引(在绘制单个轮廓时很有用。绘制所有轮廓,传递-1),其余参数是颜色,厚度等等
要绘制图像中的所有轮廓:
cv.drawContours(img, contours, -1, (0,255,0), 3)
要绘制单个轮廓,请输入四个轮廓点:
cv.drawContours(img, contours, 3, (0,255,0), 3)
但大多数时候,下面的方法会很有用:
cnt = contours[4] cv.drawContours(img, [cnt], 0, (0,255,0), 3)
注意:最后两种方法是相同的,但是当你继续前进时,你会发现最后一种方法更有用。
(3)轮廓近似方法
这是cv.findContours函数中的第三个参数。它实际上表示什么?
在上面,我们告诉轮廓是具有相同强度的形状的边界。它存储形状边界的(x,y)坐标。
但是它存储了所有坐标吗?这由该轮廓近似方法指定。
如果传递cv.CHAIN_APPROX_NONE,则存储所有边界点。
但实际上我们需要所有的积分吗?例如,你找到了直线的轮廓,你是否需要线上的所有点来表示该线?
不,我们只需要该线的两个端点。这就是cv.CHAIN_APPROX_SIMPLE的作用。它删除所有冗余点并压缩轮廓,从而节省内存。
下面的矩形图像展示了这种技术。只需在轮廓阵列中的所有坐标上绘制一个圆圈(以蓝色绘制)。
第一张图片显示了我用cv.CHAIN_APPROX_NONE(734点)获得的点数,第二张图片显示了一张带有cv.CHAIN_APPROX_SIMPLE(仅4点)的点数,它节省了多少内存!

2、轮廓特征
(1)矩
图像矩可帮助你计算某些特征,如对象的质心,对象的区域等。具体定义可以查看图像矩的维基百科页面
函数cv.moments()给出了计算的所有矩值的字典。见下文:
import numpy as npimport cv2 as cv
img = cv.imread('star.jpg',0)
ret,thresh = cv.threshold(img,127,255,0)
im2,contours,hierarchy = cv.findContours(thresh, 1, 2)
cnt = contours[0]
M = cv.moments(cnt)
print( M )
从这一刻起,你可以提取有用的数据,如面积,质心等。质心由关系给出,$C_{x}=\frac{M_{10}}{M_{00}}$和$C_{y}=\frac{M_{01}}{M_{00}}$。这可以按如下方式完成:
cx = int(M['m10']/M['m00'])
cy = int(M['m01']/M['m00'])
(2)轮廓区域
轮廓区域由函数cv.contourArea()或时刻M['m00']给出。
area = cv.contourArea(cnt)
(3)轮廓周长
轮廓周长也被称为弧长。可以使用cv.arcLength()函数找到它。第二个参数指定形状是闭合轮廓(如果传递为True),还是仅仅是曲线。
perimeter = cv.arcLength(cnt,True)
(4)轮廓近似
它根据我们指定的精度将轮廓形状近似为具有较少顶点数的另一个形状。它是Douglas-Peucker算法的一种实现方式。查看维基百科页面以获取算法和演示。
要理解这一点,可以假设你试图在图像中找到一个正方形,但是由于图像中的一些问题,你没有得到一个完美的正方形,而是一个“坏形状”(如下图第一张图所示)。现在你可以使用此功能来近似形状。在这里,第二个参数称为epsilon,它是从轮廓到近似轮廓的最大距离。这是一个准确度参数。需要选择适当的epsilon才能获得正确的输出。
epsilon = 0.1*cv.arcLength(cnt,True) approx = cv.approxPolyDP(cnt,epsilon,True)
下面,在第二幅图像中,绿线表示epsilon=弧长的10%的近似曲线。第三幅图像显示相同的epsilon=弧长的1%。第三个参数指定曲线是否关闭。

(5)凸包
凸包看起来类似于轮廓近似,但它不是(两者在某些情况下可能提供相同的结果)。这里,cv.convexHull()函数检查曲线的凸性缺陷并进行修正。
一般而言,凸曲线是总是凸出或至少平坦的曲线。如果它在内部膨胀,则称为凸性缺陷。
例如,检查下面的手形图像。红线表示手的凸包。双面箭头标记显示凸起缺陷,即船体与轮廓的局部最大偏差。
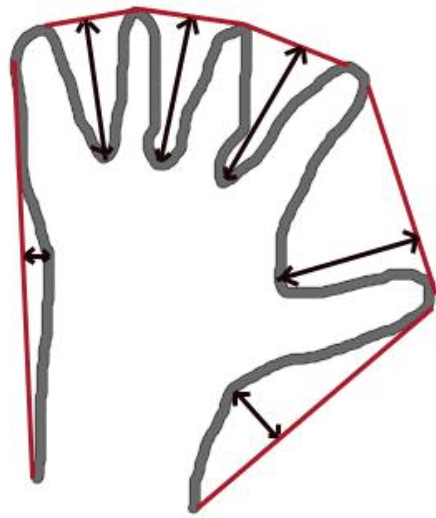
下面我们要讨论它的一些语法:
hull = cv.convexHull(points[, hull[, clockwise[, returnPoints]]
参数详情:
-
points:是我们传入的轮廓。
-
hull:是输出,通常我们忽略它。
-
clocwise:方向标志。如果为True,则输出凸包顺时针方向。否则,它逆时针方向。
-
returnPoints:默认为True。然后它返回凸包点的坐标。如果为False,则返回与凸包点对应的轮廓点的索引。
因此,为了获得如上图所示的凸包,以下就足够了:
hull = cv.convexHull(cnt)
但是如果你想找到凸性缺陷,你需要传递returnPoints = False。为了理解它,我们将采用上面的矩形图像。首先,我发现它的轮廓为cnt。现在我发现它的凸包有returnPoints = True,我得到以下值:[[234 202],[51 202],[51 79],[234 79]]这四个角落 矩形点。 现在如果对returnPoints = False做同样的事情,我得到以下结果:[[129],[67],[0],[142]]。 这些是轮廓中相应点的索引。例如,检查第一个值:cnt [129] = [[234,202]],它与第一个结果相同(对于其他结果,依此类推)。
当我们讨论凸性缺陷时,你会再次看到它。
(6)检查凸性
函数cv.isContourConvex()可以检查曲线是否凸的,它只返回True或False,没有什么理解上的问题。
k = cv.isContourConvex(cnt)
(7)边界矩形
有两种类型的边界矩形。
A.直边矩形
它是一个直的矩形,它不考虑对象的旋转。因此,边界矩形的面积不是最小的。它由函数cv.boundingRect()找到。
设(x,y)为矩形的左上角坐标,(w,h)为宽度和高度。
x,y,w,h = cv.boundingRect(cnt) cv.rectangle(img,(x,y),(x+w,y+h),(0,255,0),2)
b.旋转矩形
这里,以最小面积绘制边界矩形,因此它也考虑旋转。使用的函数是cv.minAreaRect()。它返回一个Box2D结构,其中包含以下detals - (center(x,y),(width,height),rotation of rotation)。但要画这个矩形,我们需要矩形的4个角。它是由函数cv.boxPoints()获得的
rect = cv.minAreaRect(cnt) box = cv.boxPoints(rect) box = np.int0(box) cv.drawContours(img,[box],0,(0,0,255),2)
两个矩形都显示在单个图像中。绿色矩形显示正常的边界矩形。红色矩形是旋转的矩形。

(8)最小外接圈
接下来,我们使用函数cv.minEnclosingCircle()找到对象的外接圆。它是一个完全覆盖物体的圆圈,面积最小。
(x,y),radius = cv.minEnclosingCircle(cnt) center = (int(x),int(y)) radius = int(radius) cv.circle(img,center,radius,(0,255,0),2

(9)椭圆拟合
接下来是将椭圆拟合到一个对象上。它返回刻有椭圆的旋转矩形
ellipse = cv.fitEllipse(cnt) cv.ellipse(img,ellipse,(0,255,0),2)

(10)拟合一条线
类似地,我们可以在一组点上拟合一条线。下图包含一组白点。 我们可以近似直线。

3、轮廓属性
(1)Aspect Ratio(长宽比)
它是对象的边界矩形的宽度与高度的比。
$$Aspect\ Ratio= \frac{Width}{Height}$$
x,y,w,h = cv.boundingRect(cnt) aspect_ratio = float(w)/h
(2)Extent(大小比)
它是轮廓区域与边界矩形区域的比。
$$Extent= \frac{Object\ Area}{Bounding\ Rectangle\ Area}$$
area = cv.contourArea(cnt) x,y,w,h = cv.boundingRect(cnt) rect_area = w*hextent = float(area)/rect_area
(3)Solidity(密实比)
Solidity是轮廓区域与其凸包区域的比率。
$$Solidity= \frac{Contour\ Area}{Convex\ Hull\ Area}$$
area = cv.contourArea(cnt) hull = cv.convexHull(cnt) hull_area = cv.contourArea(hull) solidity = float(area)/hull_area
(4)Equivalent Diameter(等效直径)
等效直径是圆的直径,其面积与轮廓面积相同。
$$Equivalent\ Diameter=\sqrt{\frac{4\times Contour\ Area}{\pi }}$$
area = cv.contourArea(cnt) equi_diameter = np.sqrt(4*area/np.pi)
(5)Orientation(方向)
方向是对象定向的角度。以下方法还给出了主轴和短轴长度。
(x,y),(MA,ma),angle = cv.fitEllipse(cnt)
(6)Mask & Pixel Points(掩模和像素点)
在某些情况下,我们可能需要包含该对象的所有点。它可以如下完成:
mask = np.zeros(imgray.shape,np.uint8) cv.drawContours(mask,[cnt],0,255,-1) pixelpoints = np.transpose(np.nonzero(mask)) #pixelpoints = cv.findNonZero(mask)
这里,两个方法,一个使用Numpy函数,另一个使用OpenCV函数(最后一个注释行)给出相同的方法。 结果也相同,但略有不同。 Numpy以**(行,列)格式给出坐标,而OpenCV以(x,y)**格式给出坐标。所以答案基本上会互换。请注意,row=x和column=y。
(7)最大值,最小值及其位置
我们可以使用掩模图像找到这些参数。
min_val, max_val, min_loc, max_loc = cv.minMaxLoc(imgray,mask = mask)
(8)平均颜色或平均灰度
在这里,我们可以找到对象的平均颜色。或者它可以是灰度模式下物体的平均强度。我们再次使用相同的面具来做到这一点。
mean_val = cv.mean(im,mask = mask)
(9)极点
极值点表示对象的最顶部,最底部,最右侧和最左侧的点。
leftmost = tuple(cnt[cnt[:,:,0].argmin()][0]) rightmost = tuple(cnt[cnt[:,:,0].argmax()][0]) topmost = tuple(cnt[cnt[:,:,1].argmin()][0]) bottommost = tuple(cnt[cnt[:,:,1].argmax()][0])
例如,如果我将它应用于印度地图,我会得到以下结果:
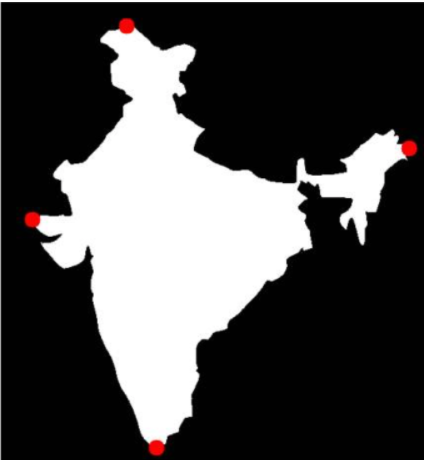
(2)点多边形测试
此功能可查找图像中的点与轮廓之间的最短距离。当点在轮廓外时返回负值,当点在内部时返回正值,如果点在轮廓上则返回零。
例如,我们可以检查点(50,50)如下:
dist = cv.pointPolygonTest(cnt,(50,50),True)
在函数中,第三个参数是measureDist。如果为True,则查找签名距离。如果为False,则查找该点是在内部还是外部或在轮廓上(它分别返回+1,-1,0)。
注意:如果你不想找到距离,请确保第三个参数为False,因为这是一个耗时的过程。因此,将其设为False可提供2-3倍的加速。
(3)匹配形状
OpenCV附带了一个函数cv.matchShapes(),它使我们能够比较两个形状或两个轮廓,并返回一个显示相似性的度量。结果越小,匹配就越好。它是根据hu-moment值计算的。文档中解释了不同的测量方法。
import cv2 as cvimport numpy as np img1 = cv.imread('star.jpg',0) img2 = cv.imread('star2.jpg',0) ret, thresh = cv.threshold(img1, 127, 255,0) ret, thresh2 = cv.threshold(img2, 127, 255,0) im2,contours,hierarchy = cv.findContours(thresh,2,1) cnt1 = contours[0] im2,contours,hierarchy = cv.findContours(thresh2,2,1) cnt2 = contours[0] ret = cv.matchShapes(cnt1,cnt2,1,0.0) print( ret )
我尝试匹配下面给出的不同形状的形状:

我得到了以下结果:
匹配图像A与其自身= 0.0 匹配图像A与图像B = 0.001946 匹配图像A与图像C = 0.326911 请注意,即使图像旋转对此比较也没有太大影响。
也可以看看 Hu-Moments是对翻译,旋转和缩放不变的七个时刻。第七个是偏斜不变的。可以使用cv.HuMoments()函数找到这些值。
5、轮廓层次结构
(1)理论
在最近几篇关于轮廓的文章中,我们使用了与OpenCV提供的轮廓相关的几个函数。但是当我们使用cv.findContours()函数在图像中找到轮廓时,我们已经传递了一个参数Contour Retrieval Mode。我们通常传递cv.RETR_LIST或cv.RETR_TREE,它运行的效果很好。但它究竟意味着什么?
此外,在输出中,我们得到三个数组,第一个是图像,第二个是我们的轮廓,还有一个我们命名为层次结构的输出(请查看以前文章中的代码)。但我们从未在任何地方使用过这种层那么这个层次结构又是什么呢?它与前面提到的函数参数有什么关系?
这就是我们将在本文中处理的内容。
什么是层次结构?
通常我们使用cv.findContours()函数来检测图像中的对象,对吧?有时对象位于不同的位置。但在某些情况下,某些形状在其他形状内。就像嵌套的数字一样。在这种情况下,我们将外部一个称为父项,将内部项称为子项。这样,图像中的轮廓彼此之间存在某种关系。我们可以指定一个轮廓如何相互连接,例如,它是某个其他轮廓的子项,还是父项等。这种关系的表示称为层次结构。
考虑下面的示例图片:
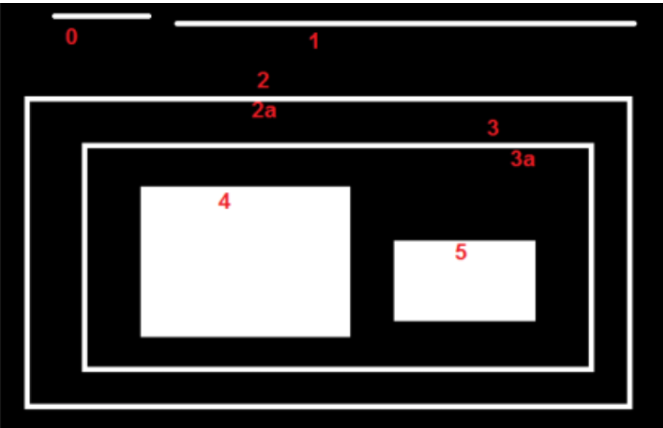
在这张图片中,有一些形状,我从0-5编号。图2和2a表示最外侧盒子的外部和内部轮廓。
这里,轮廓0,1,2是外部或最外部的。我们可以说,它们在层次结构0中,或者只是它们处于相同的层次结构级别。
接下来是轮廓-2a。它可以被认为是轮廓-2的子节点(或者相反,轮廓-2是轮廓-2的父节点)。所以让它在层次结构-1中。类似地,轮廓-3是轮廓-2的子,它进入下一层次。最后,轮廓4,5是轮廓-3a的子节点,它们位于最后的层次结构级别。从我编号框的方式,我会说轮廓-4是轮廓-3a的第一个孩子(它也可以是轮廓-5)。
我提到这些东西来理解相同的层次结构,外部轮廓,子轮廓,父轮廓,第一个孩子等术语。现在让我们进入OpenCV。
OpenCV中的层次结构表示
因此每个轮廓都有自己的信息,关于它是什么层次结构,谁是它的子,谁是它的父等.OpenCV将它表示为四个值的数组:[Next,Previous,First_Child,Parent]
“下一个表示同一层级的下一个轮廓。”
例如,在我们的图片中取出contour-0。谁是同一水平的下一个轮廓?它是轮廓-1。所以简单地说Next = 1.类似地,对于Contour-1,next是contour-2。所以Next = 2。
轮廓-2怎么样?同一级别没有下一个轮廓。所以简单地说,将Next = -1。轮廓-4怎么样?它与contour-5处于同一水平。所以它的下一个轮廓是轮廓-5,所以Next = 5。
“上一个表示同一层级的先前轮廓。”
与上述相同。轮廓-1的先前轮廓在同一水平面上为轮廓-0。类似地,对于轮廓-2,它是轮廓-1。而对于contour-0,没有先前的,所以把它作为-1。
“First_Child表示其第一个子轮廓。”
无需任何解释。对于轮廓-2,孩子是轮廓-2a。因此它获得了contour-2a的相应索引值。轮廓-3a怎么样?它有两个孩子。但我们只带第一个孩子。它是轮廓-4。因此,对于轮廓-3a,First_Child = 4。
“父表示其父轮廓的索引。”
它与First_Child相反。对于轮廓-4和轮廓-5,父轮廓都是轮廓-3a。对于轮廓-3a,它是轮廓-3,依此类推。
注意:如果没有子项或父项,则该字段将被视为-1
所以现在我们知道OpenCV中使用的层次结构样式,我们可以在上面给出的相同图像的帮助下检查OpenCV中的Contour Retrieval Modes。即cv.RETR_LIST,cv.RETR_TREE,cv.RETR_CCOMP,cv.RETR_EXTERNAL等标志是什么意思?
(2)轮廓检索模式
-
RETR_LIST
这是四个标志中最简单的(从解释的角度来看)。它只是检索所有轮廓,但不创建任何父子关系。根据这条规则,父和子是平等的,他们只是轮廓。即它们都属于同一层次结构。
所以这里,层次结构数组中的第3和第4项始终为-1。但显然,Next和Previous术语将具有相应的值。请自行检查并验证。
下面是我得到的结果,每行是相应轮廓的层次结构细节。例如,第一行对应于轮廓0.下一个轮廓是轮廓1.所以Next = 1.没有先前的轮廓,所以Previous = -1。如前所述,剩下的两个是-1。
>>> hierarchy array([[[ 1, -1, -1, -1], [ 2, 0, -1, -1], [ 3, 1, -1, -1], [ 4, 2, -1, -1], [ 5, 3, -1, -1], [ 6, 4, -1, -1], [ 7, 5, -1, -1], [-1, 6, -1, -1]]])
如果你没有使用任何层次结构功能,这是在代码中使用的不错选择。
-
RETR_EXTERNAL
如果使用此标志,则仅返回极端外部标志。所有儿童轮廓都被遗忘。我们可以说,根据这项法律,只有每个家庭中最年长的人才能得到照顾。它并不关心其他家庭成员:)。
那么,在我们的图像中,有多少极端外轮廓?即在等级0级?只有3个,即轮廓0,1,2,对吧?现在尝试使用此标志查找轮廓。这里,给予每个元素的值与上面相同。将其与上述结果进行比较。以下是我得到的:
>>> hierarchyarray([[[ 1, -1, -1, -1], [ 2, 0, -1, -1], [-1, 1, -1, -1]]])
如果只想提取外轮廓,可以使用此标志。在某些情况下它可能有用。
-
RETR_CCOMP
此标志检索所有轮廓并将它们排列为2级层次结构。即对象的外部轮廓(即其边界)放置在层次结构-1中。对象内部的孔的轮廓(如果有的话)放在层次结构-2中。如果其中有任何对象,则其轮廓仅再次放置在层次结构-1中。它在层次结构-2中的漏洞等等。
只需考虑黑色背景上的“大白零”图像。零的外圆属于第一层次,零的内圈属于第二层次。
我们可以用简单的图像来解释它。在这里,我用红色(1或2)标记了红色轮廓的顺序和它们所属的层次结构。订单与OpenCV检测轮廓的顺序相同。
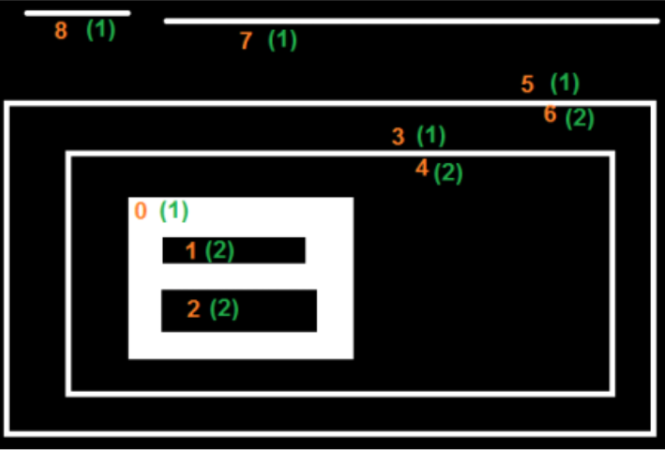
因此,考虑第一个轮廓,即轮廓-0。它是层次结构-1。它有两个孔,轮廓1和2,它们属于层次结构-2。因此对于轮廓-0,相同层级中的下一轮廓是轮廓-3。并且之前没有。它的第一个是子级是层次结构-2中的轮廓-1。它没有父级,因为它位于层次结构-1中。所以它的层次结构数组是[3,-1,1,-1]
现在采取轮廓-1。它在层次结构-2中。同一层次中的下一个(在轮廓-1的父下面)是轮廓-2。没有前一个。没有子,但父是轮廓-0。所以数组是[2,-1,-1,0]。
类似于contour-2:它在层次结构-2中。在contour-0下,同一层次中没有下一个轮廓。所以没有下一个。以前是轮廓-1。没有子,父是轮廓-0。所以数组是[-1,1,-1,0]。
轮廓-3:层次结构-1中的下一个是轮廓-5。上一个是轮廓-0。子是轮廓4而没有父。所以数组是[5,0,4,-1]。
轮廓 - 4:它在等高线3中的等级2中,并且没有兄弟。所以没有下一个,没有先前,没有子,父是轮廓-3。所以数组是[-1,-1,-1,3]。
剩下的你可以填写。这是我得到的最终答案:
>>> hierarchyarray([[[ 3, -1, 1, -1], [ 2, -1, -1, 0], [-1, 1, -1, 0], [ 5, 0, 4, -1], [-1, -1, -1, 3], [ 7, 3, 6, -1], [-1, -1, -1, 5], [ 8, 5, -1, -1], [-1, 7, -1, -1]]])
-
RETR_TREE
这是最后一个人,Mr.Perfect。它检索所有轮廓并创建完整的族层次结构列表。它甚至告诉,谁是爷爷,父,子,孙子,甚至超越...... :)。
例如,我拍摄了上面的图像,重写了cv.RETR_TREE的代码,根据OpenCV给出的结果重新排序轮廓并进行分析。同样,红色字母给出轮廓编号,绿色字母给出层次结构顺序。
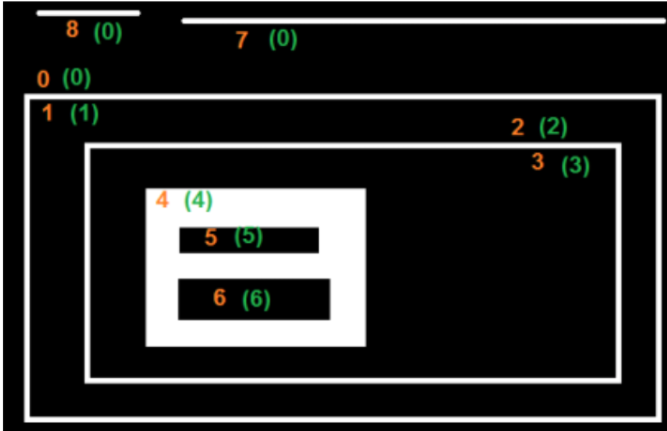
取contour-0:它在层次结构-0中。 同一层次中的下一个轮廓是轮廓-7。没有以前的轮廓。子是轮廓-1。 没有父。 所以数组是[7,-1,1,-1]。
取等高线2:它在层次结构-1中。同一级别没有轮廓。没有前一个。子是轮廓-3。父是轮廓-1。所以数组是[-1,-1,3,1]。
剩下的,试试吧。 以下是完整的答案:
>>> hierarchyarray([[[ 7, -1, 1, -1], [-1, -1, 2, 0], [-1, -1, 3, 1], [-1, -1, 4, 2], [-1, -1, 5, 3], [ 6, -1, -1, 4], [-1, 5, -1, 4], [ 8, 0, -1, -1], [-1, 7, -1, -1]]])
 同乐学堂
同乐学堂
 微信扫一扫,打赏作者吧~
微信扫一扫,打赏作者吧~
